Three-Bar LinkageJ

4節リンク機構

二つ目のチュートリアルでは、簡単なリンク機構のダイナミクスを見てみましょう。 特に、長さ一定の線分の作り方、幾何学的軌跡の描き方について学ぶことができるでしょう

棒(長さ一定の線分)を作る

シンデレラをスタートさせて(または前に書いたものをすべて消去して) 半径つき円 モードにするために ボタンを押してください。 このモードは、中心と半径を指定して円を描くときに用いられます。 マウスを描画面の上に動かして、(左)ボタンを押してください。 そのままマウスをドラッグさせれば、中心が固定されたまま、円が現れます。 適当なところでボタンを離してください。 この動作だけで、描画面上に円を描くことができます。 モードを 動かすモード にして、この円の中心をドラッグして動かしてみましょう。 円は半径を一定にしたまま形を変えずに動くことがわかるでしょう。 また、円周自身をドラッグして動かしてみると、中心を固定したまま半径が変わるのがわかるでしょう。

図1：一つ目の円

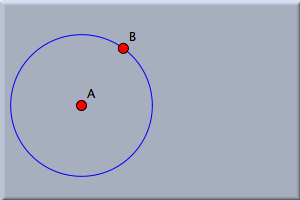
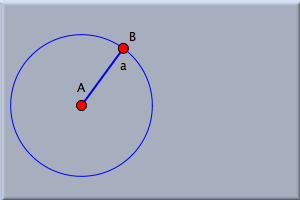
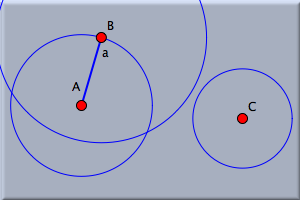
それでは、今描いた円周上に新しく点を追加しましょう。 点を加える モードにして、マウスを描画面へ動かします。 そこでマウスを押すと新しく点が現れますが、それをドラッグして円周にスナップしてみましょう。 (近づけてみると、マウスがぱちん、という感じで重なるのがわかります。 これがスナップです。) 円周が白く光って、そこでボタンを離せば円周上に点が描かれます。 こうやって、円周上に存在する点を作り出すことができました。 もちろん、そのかわりに円周上でマウスをクリックしても点を作ることができます。 しかし、この方法だと、マウスのコントロールを間違えると点が正しく円周上に乗っていないこともありえます。 はじめに述べた方法のほうが、わずかのコントロールですむのです。 この結果、図１のような図形が作図されているでしょう。

動かすモード にして、今描いたばかりの点をドラッグして動かしてみましょう。 もし、点が円周上に乗っていれば、点は円周から離れないのがわかります (もしそうでなかったら、ひとつ戻ってやり直しましょう)。 この制限の下で、点はマウスにできるだけ近い場所に位置するように動きます。 もし円の中心を移動したり、円の半径を変えたとしてもこの点が円周から離れることはありません． このとき点は中心からの角度を保つところに位置します。 ツールボタンを押して add a segmentJ モードにして、円の中心Aから円周上の点Bまで線分を引きます。 __ (図2を見てください)。

図2：棒

こうすると、この線分は長さが一定(半径の長さに等しい)の棒のように振舞います。 棒の長さを変えるには、円の半径を変えればいいのです。

もう2本の棒を追加する

さて、もう2本の棒を追加して、「動的な幾何学」の節に出てきたような4節リンク機構の図を完成させましょう。 リンク機構とは、長さ一定の棒で、両端が別々の装置につながっているものをいいます。 半径つき円 モードに切り替えます。 そして最初の円のやや右側に二つ目の円を描きましょう。 このとき、最初の円と交わらないように描きます。

この二つ目の円の半径は一番右の三番目の棒(まだ第二番目の棒も描かれていないのですが)の長さのためのものです。 作図を完成させるために状況を解析してみるとよいでしょう。 点 C から点 B へと長さの決まった2本の棒で連結すると、棒のつながっている点にはそれほど自由度がないことになります。 実際、この点の可能性はちょうど2通りしかありません． つまり、二つの円(ひとつは点 C を中心にした円ですでに描いてあります。 もうひとつは点 B を中心にした円)の交点(一般には2箇所)がその点です。

図3：さらに2つの円

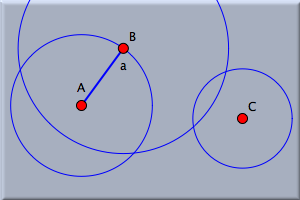
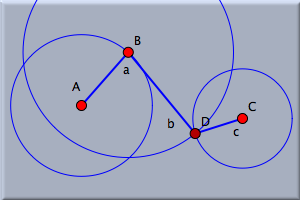
次に、 点 B を中心として円を描いてみましょう。 半径つき円 モードを使います。 半径を十分大きく取り、点 C を中心とする円と交わるようにします。 図3にこの図が描かれています。 最後に、 線分を加える モード で、点 B と、円の交点（ B を中心とした円と、点 C を中心とした円の交点のうちの1つ）とを結ぶ直線を描きます。

図4：全部で3本の棒

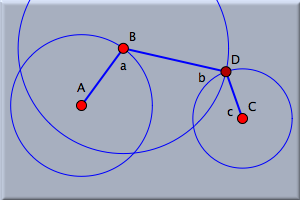
この新しい点は自動的に D と名前が付けられます。 この新しい点は自由に動ける点ではなく、A、B、C の場所と、円の半径から決まることに注意します。


図を完成させるために、点 C と点 Dとを結ぶ線分を描きましょう。 図4のようになったでしょうか。

図を動かしてみる

棒(線分)の長さは、円の半径から決まります。 動かすモード にして、この図で遊んでみましょう。 点 B を最初の円に沿って動かすと面白いことになります。

図5：棒が短すぎた例

まず最初に、点 B を動かすことにより、図全体はちょうど1次元の自由度を持つことがわかります。 点 B を動かすと、図全体はあたかも接続された棒のような機械的な動きを見せます。 点 B の動かせる範囲は、ＣＡＤで言うところの駆動入力 (訳註：外部からモータなどで動力を伝達して装置を稼動させる部分) のようなものになっています。 点 B の場所によっては真中の棒の長さが足りないような場合があります。(図5を見てください) つまり、二つの円が交わらない場合です。 このとき、交点や線分(のいくつか)は消えてしまいます。

図6：点 B を元に戻す

点 B を最初の位置に戻したとき、もっとも興味深いことが起こります。 最初は見落としてしまったかもしれません． それは、点 D が、最初に選んだのとは別の交点になっていることです。 そしてリンク機構の配置は、2通りある可能性のうちのもう一方に変わっています。 このことは、何回か試してみるとその感じがつかめると思います。 点 B をもう一度動かしてみましょう。 線分は一度消え、そしてまた現れます。 この現象は、最初はあなたの直観と合わないかもしれません。 しかし、これはきわめて正常な出来事なのです。 これらの線分が実際に鉄や木でできていることを考えてみましょう。 これらには質量があるわけです。 慣性の力だけで棒を自由に動かしたとすると、何がおこるでしょうか． 画面上で線分が消えてしまうところにくると、実際の2本の棒は一直線に並ぶことがわかります。 そして、点 D は「ひきずられ」、図全体はもう一つの可能な状況へと移行することがわかります。

アニメーションを始める

さて、もしあなたが以上の状況が自然なものであるとまだ信じられないならば、 アニメーション モードにするために ボタンを押してください。 ウィンドウ下方のメッセージには、動かす点を選ぶように指示が出ます。 私たちは、点 B を動かしたいのですから、点 Bをクリックします。 点 B は自由度1で動かすことができる点ですから、点 B を動かす道はおのずと明らかです。 ですから、アニメーションはすぐに始まります。 もし指定した点がどの道の上を動くのかはっきりしない場合には、点 B を動かす道を指定する必要があります。 今の場合には、動かす道は明らかに最初に描いた円であることがわかるので、指定する必要はありません。

アニメーションを制御するウィンドウが現れます。


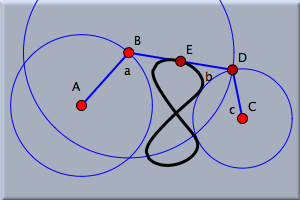
そこには、CDプレーヤでよく見かけるのと同じように、アニメーションの開始、停止、一時停止ボタンがあります。 それと、アニメーションのスピードを変えるためのスライダがあります。 プレイボタンを押してアニメーションを始めましょう。

しばらく、アニメーションを見てみましょう。点 B を観察していると、3本の線分を描くことができる範囲でのみ動いていることがわかるでしょう。 どこで方向を切り替えるべきか(シンデレラは)わかっているのです。 シンデレラ は、物理的な振舞いを再現するように作られています。 動く要素に質量を与えているのではなく、複素解析の手法を用いて理にかなった振舞いを見つけているのです。アニメーションが続く間に自由要素を動かすこともできます。では、ストップボタンを押してアニメーションを終わりましょう。

軌跡を描く

さて、真中の線分の中点がアニメーションでどのような動きをするのか、見てみましょう。 まず、その中点を図に追加します。 中点 モードにするために ボタンを押してください。 マウスボタンを「押す、ドラッグする、離す」という一連の動作によって、任意の2点の中点を作図することができます。 マウスを点 D の上に持ってきて、マウスボタンを押します。 ボタンを押したままドラッグしてマウスを点 B の上まで持ってきて、そして離します。 こうすることによって、中点が図に追加されます。

さて、次に 軌跡 モードにするために ボタンを押してください。 このモードでは、「動かす点」、「動かす道」、「軌跡を描く点」の3つをこの順に指定する必要があります。 動かす点とは動く要素(駆動力)で、動かす道とは、文字通り動かす点の動く道であり、これは動かす点に対し適切に定まっていなくてはなりません． 軌跡を描く点の軌道が計算されて表示されるというわけです。

点 B (動かす点)をまずクリックします。 シンデレラは指定された動かす点の自由度が1だった場合、動かす道を認識し選択します。そこで 点 E をクリックします。これが軌跡を描く点と認識されます。 すこし待つと、 自動的に軌跡が計算されて表示されます。 ここで、点を動かすモードにして、自由要素を動かしてみると軌跡がどのように変化するのかをみることができます。

軌跡の描画

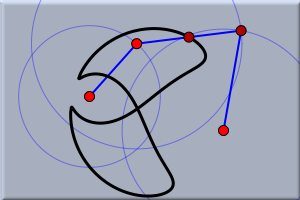
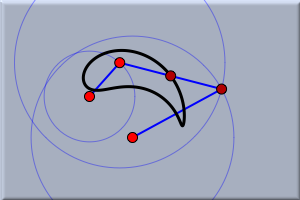
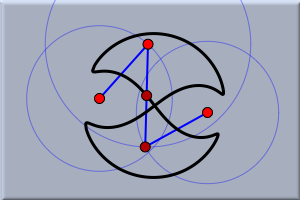
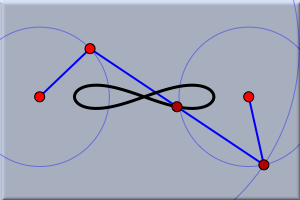
ここで、プレイボタンを押してアニメーションを再開すれば、 どのように軌跡が得られたかを見ることができます。

実験

　でき上がった図で実験をしてみましょう。今できた軌跡は、自由点A,Cの位置（円の中心）とB(半径AB)を変えることによって変化します。次の図で示すように面白く、ときにはびっくりするような図形ができるでしょう。






(阿原・入谷)