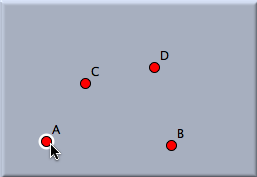
Similarity

Similarity

Similarities are among the most useful transformations available in Cinderella. They can be considered as a composition of a rotation and a scaling. With a suitably chosen similarity one can map an arbitrary (ordered) pair of points to another one.

A similarity can be defined by specifying the preimage and image for two pairs of sample points. Thus a similarity is defined by choosing an (ordered) collection of four points.

First click: The first preimage is defined.		Second click: The first image is defined.		Third click: The second preimage is defined.		Fourth click: The second image is defined.

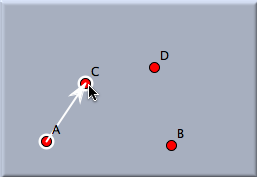
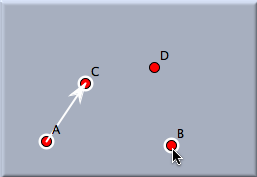
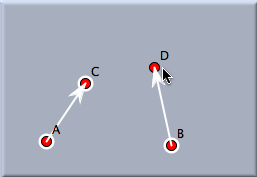
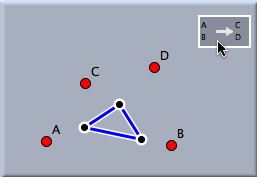
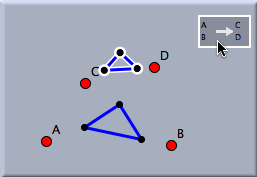
After this sequence of four clicks, the similarity has been defined completely. In this example the similarity will be uniquely defined by the facts that A is mapped to C and that B is mapped to D.

Applying a translation to a selection of many objects will map them all simultaneously. The following pictures demonstrate the effect of a similarity transformation.

The preimage		The situation after mapping

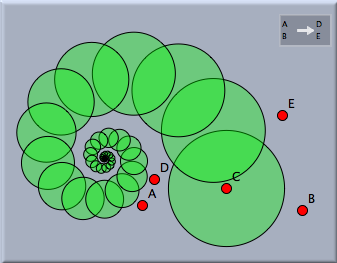
If one iterates a similarity, the sequence of mapped pictures will automatically form some kind of logarithmic spiral. The picture below demonstrates this effect.

A logarithmic spiral

In the definition of a similarity it is also possible to use points more than once. Thus it is possible to map a point to itself by selecting the same point as image and preimage. We get several interesting special cases of similarity:

• A → A and B → B: The identity transformation, which leaves all points invariant
• A → A and B → C: A similarity, with fixed point A
• A → B and B → A: A point reflection that interchanges A and B

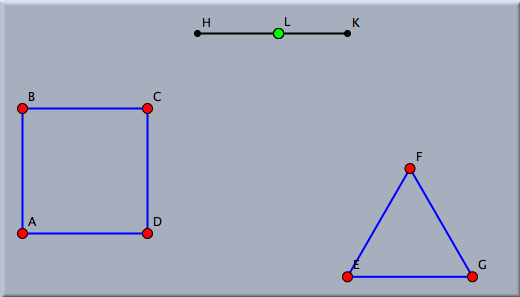
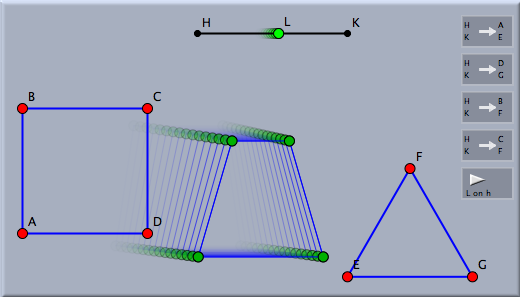
Similarities and Sliders

Similarities are sometimes very useful tools for implementing a slider control in a geometric scenario. The following example illustrates this technique. Suppose that you want to create an object that can be smoothly transformed from one shape into another. The transition is to be controlled by a point on a segment that acts as a slider control. Let us suppose that you want to create a figure that "morphs" from the square on the left smoothly to the triangle on the right as the green point is moved.

A morphing task

One can achieve such an effect by defining many similarity configurations, one for each preimage/image pair of points. For each such pair one defines a similarity that maps the endpoints of the slider to the two points of the pair. One then constructs the image of the sliding point under this map. When the slider is moved, the mapped point moves from the morphing start position smoothly to the end position. The picture below shows a construction of this process.

Morphing made easy