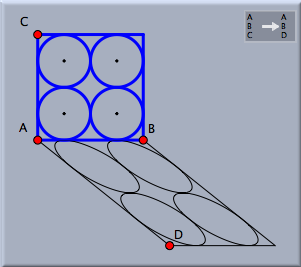
Affine Transformation

Affine Transformation

An affine transformation is something between a similarity and a projective transformation. A similarity preserves the angle between two lines, but this is no longer the case for an affine transformation. However, parallelism is preserved by affine transformations, which is not the case for projective transformations.

An affine transformation is defined by three preimage/image pairs of points. The definition is analogous to that of a similarity, though with six required points instead of four.

The picture below shows a simple scene in which a blue figure is mapped affinely to a black figure.

Application of an affine transformation