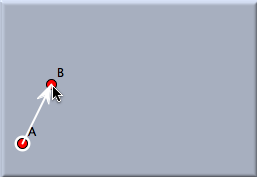
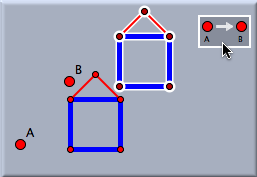
Translation

Translation

A translation is a shift in a certain direction by a particular length. A translation is defined by selecting two points that serve as a sample of a preimage and an image. Defining the translation requires two mouse clicks.

First selection: The first point of the translation is selected		Moving the mouse: An arrow hint is shown.		Move to second point: The arrow helps you.		Second selection: The translation is created.

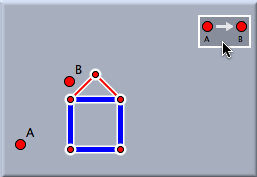
A detailed description of defining a translation can be found in the section General Use of Transformations.

Applying a translation to a selection of many objects will map them all simultaneously. In this process all appearance information is transferred from the preimages to the images. The following pictures demonstrate how appearance information is transferred.

The preimage		Situation after mapping

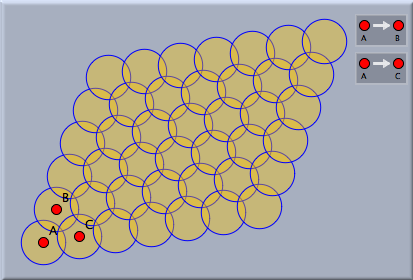
One use of translations is to create regular ornamental patterns. The following picture shows a pattern that is generated by the repeated application of two translations in two different directions.

A regular pattern of circles

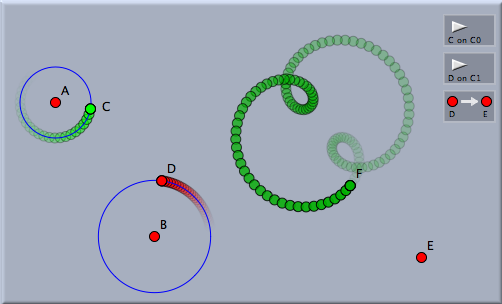
Transformations may also be used in order to study a certain situation that occurs locally around a moving point. In such a situation one may introduce another point as a kind of fixed base point, define a translation that maps the point of interest to this point and finally maps the point whose relative movement is to be studied with this translation. Since this application of transformations may appear slightly advanced, we give a little example of this technique. Consider the image below. There a rotating red point D and a rotating green point C are shown. The green point rotates three times as fast as the red one. What is the trace of the green point viewed from the rotating red point. For this, a transformation is defined that maps the red point D to some fixed point E. Then the map is applied to the green point. The trace of the mapped point is shown as a dark-green trace. This is how D sees C.

Analyzing from different perspectives

The same technique has been used in the section Geometry and CindyLab, in Example 2, where the behavior of the velocity vector in planetary motion was analyzed.