Elementary Drawing FunctionsJ描画関数の基礎この節で解説するのは、点、直線、線分を描く演算子です。 描画:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 表記: | 描画: | |
draw([x,y]) | x,y座標に点を打つ | |
draw([x,y,z]) | 同次座標が (x,y,z) である点を打つ。(これについてはこのあとに説明があります) | |
同次座標について:
[x,y,z] が点の同次座標であるとき、対応する点は、 xy-座標が [x/z,y/z] の点です。 z=0 の点は "無限遠点" です。この点は、シンデレラの通常のユークリッド表示では見えません。しかし、球面表示や局所的に射影基底が設定されている場合は表示されます。(参照 : 座標系).線分を描く:2点のリストを与えると線分を描きます。 点の座標はユークリッドの座標でも、同次座標でもかまいません。
| 表記: | 描画: | |
draw([a,b]) | a と b を結ぶ線分を引く
| |
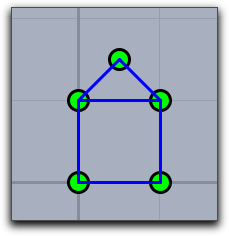
例: 次のコードは、次の図を描きます。ユークリッドの座標と同次座標の両方が使われています。さらに、線分の描画命令が点の描画命令のあとにあるので、線分の方が前面に描かれています。
A=[0,0]; B=[0,2,2]; C=[1,1,1]; D=[1,0]; E=[0.5,1.5]; linesize(3); pointsize(10); draw(A);draw(B); draw(C);draw(D);draw(E); draw([A,B]);draw([B,C]); draw([C,D]);draw([D,A]); draw([C,E]);draw([B,E]);
 |
直線を描く: 同次座標は直線を表すの用いられます。3つの実数
[a,b,c] で表される直線は、方程式 a∗x+b∗y+c=0で表されるものと考えることができます。 ユークリッド座標 [x,y]の点は、この方程式を満たすときに限りこの直線上にあります。同次座標 [x,y,z]の点は、方程式 a∗x+b∗y+c∗z=0 を満たすときに限りこの直線上にあります。3つの実数
[a,b,c]が点を表すのか直線を表すのかをCindyScriptが知るために、直線が引かれた場合には内部フラグが立つようになっています。たとえば、 join(A,B)命令は、2点 A と B を通る直線を計算して、直線であるという内部フラグを立てます。その結果、直線が引かれます。演算子 line() を使うことによって、直線のフラグを強制的に立てることもできます。例: 次の2つの描画命令はいずれも直線を描きます:
draw(line([1,1,0.5])); draw(join([1,2],[2,-1]));
修飾子: 描画命令はいくつかの修飾子を扱うことができます。それらを次の表にまとめます。
| 修飾子: | 値の型 | 効果: |
pointsize | <実数> | 点の大きさを設定する。 |
linesize | <実数> | 線の幅を設定する |
size | <実数> | 点の大きさと線の幅を設定する |
pointcolor | [<実数1>,<実数2>,<実数3>] | RGB 値による点の色を設定する |
linecolor | [<実数1>,<実数2>,<実数3>] | RGB 値による線の色を設定する |
color | [<実数1>,<実数2>,<実数3>] | RGB 値による点と線の色を設定する |
alpha | <実数> | 透明度を |
noborder | <ブール値> | noborder->true なら点の境界線の表示をしない
|
border | <ブール値> | border->true なら点の境界線の表示をする
|
dashtype | <実数> | 破線パターンを0から4で指定する |
dashing | <実数> | 破線を描く。与えた数により細かさが変わる |
dashpattern | <リスト> | 個別の破線パターンを指定する |
修飾子は部分的な効果です。つまり、表示に関する初期設定は修飾子があるときは無効で修飾子が優先されます。
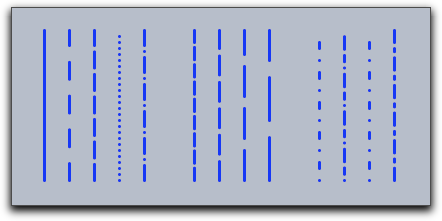
例: 次のコードは、破線の修飾子を使った例です。
linesize(3); draw((0,0),(0,6),dashtype->0); draw((1,0),(1,6),dashtype->1); draw((2,0),(2,6),dashtype->2); draw((3,0),(3,6),dashtype->3); draw((4,0),(4,6),dashtype->4); draw((6,0),(6,6),dashing->4); draw((7,0),(7,6),dashing->6); draw((8,0),(8,6),dashing->8); draw((9,0),(9,6),dashing->10); draw((11,0),(11,6),dashpattern->[0,4,2,4]); draw((12,0),(12,6),dashpattern->[0,2,2,2,4,2]); draw((13,0),(13,6),dashpattern->[0,4,2,4]); draw((14,0),(14,6),dashpattern->[4,2,1,2]);
 |
参照:: 座標系 と 幾何学演算子
線分を引く: draw(<expr>,<expr>)
説明: draw演算子に2つの引数を与えると線分が描けます。2つの引数はユークリッド座標か同次座標です。したがって、
[draw([0,0],[1,1])] は [0,0] to [1,1] を結ぶ線分を描きます。修飾子:
draw(<expr>) と同様、いくつかの修飾子が使えます。ただし、点に関する指定は無効です。リストのオブジェクトを描画する: drawall(<list>)
説明:
drawall(<list>) 演算子は、リストを引数とします。リストのそれぞれの要素は、通常の draw(<expr>) 演算子で描画できるものでなくてはなりません。 drawall 演算子は数学的に複雑な、あるいは高度に規則性のある図形を描くのにとても役に立ちます。例: 次のコードは、次の図を描きます。2行目で単位円上に点を打つ関数を定義します。
steps=2*pi*(1..n)/n; 行は、変数 steps を単位円を17等分する角度のリストとして作ります。これらに対応する点が、変数 pts に pts=apply(steps,f(#)) の行でリストとして代入されます。変数 segs はこのような点のすべてのペアのリストです。最後の2つの行で、 draw を使って、このリストにある線分を描きます。n=17; f(x):=[sin(x),cos(x)]; steps=2*pi*(1..n)/n; pts=apply(steps,f(#)); segs=pairs(pts); drawall(segs,alpha->0.9); drawall(pts,size->4);
 |
修飾子: この演算子は
draw(<expr>) 演算子と同様な修飾子を扱います。点をつなげる: connect(<list>)
説明: この演算子は、点のリストを受け取って、それらを順に結んだ線分を描きます。
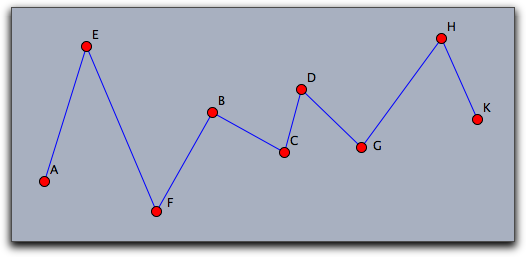
例: 次のコードは、シンデレラで画面上に描かれたすべての点に対し、点を順に結んだ図を描きます。1行目で変数
pts に、描かれているすべての点を代入します。2行目で、変数 sortpts に x-座標で並べ替えた点のリストを代入します。最後に、 connect演算子で点を順に結びます。pts=allpoints(); sortpts=sort(pts,#.x); connect(sortpts);
 |
修飾子: この演算子は
draw() 演算子と同様な修飾子を扱います。多角形を描く: drawpoly(<list>)
説明: この演算子は、点のリストを受け取って、それらからできる多角形を描きます。
修飾子: この演算子は次の修飾子が使えます。
| 修飾子: | 値の型 | 効果: |
color | [<実数1>,<実数2>,<実数3>] | 点の色と線の色を RGB 値で与える |
alpha | <実数> | 透明度を指定する |
中を塗った多角形を描く: fillpoly(<list>)
説明: この演算子は、点のリストを受け取って、それらからできる中が塗られた多角形を描きます。
例: 次のコードはそのあとのような図を描きます。
repeat ループのそれぞれのステップで長方形を描き、そののち、座標系を回転・縮小しています。sq=[[-1,-1],[-1,1],[1,1],[1,-1]]; repeat(300,i, fillpoly(sq,color->hue(i/10)); rotate(4°); scale(0.95); )
 |
修飾子: 次の修飾子が使えます。:
| 修飾子: | 値の型 | 効果: |
color | [<実数1>,<実数2>,<実数3>] | RGB値で点と線の色を指定する。 |
alpha | <実数> | |
円を描く: drawcircle(<point>,<radius>)
説明:
<point> を中心とする半径 <radius> の円を描きます。点の座標はユークリッド座標か同次座標で与えます。修飾子: この関数は
draw(<expr>) と同様な修飾子ガ使えます。円盤を描く: fillcircle(<point>,<radius>)
説明:
<point> を中心とする、半径 <radius> の、内部を塗りつぶした円を描きます。点の座標はユークリッド座標か同次座標で与えます。修飾子: この関数は次の修飾子が使えます。:
| 修飾子: | 値の型 | 効果: |
color | [<実数1>,<実数2>,<実数3>] | 塗りつぶす色を RGB 値で与える |
alpha | <実数> | 透明度を指定する |
例: 次の例が
drawcircle と fillcircle を使った例です。repeat(100,i, fillcircle((0,0),1,color->hue(i/70)); drawcircle((0,0),1,color->(0,0,0)); translate((1.5,0));rotate(26°);scale(.95); );
 |
Contributors to this page: Akira Iritani
and
Kortenkamp
.
Page last modified on Tuesday 06 of March, 2012 [10:53:41 UTC] by Akira Iritani.
The content on this page is licensed under the terms of the License.
Login