Geometric OperatorsJ幾何学的演算幾何学的演算は、幾何の基本的な操作を演算として行うものです。それは、図形の要素や位置を表すベクトル(数のリスト)に適用されます。もし、演算子が図形の要素を返すならば、それをdraw演算子で描画することもできます。 リストと座標直線のための座標は常に同次座標です。すなわち、3つの数のリストで、 [a,b,c] が、方程式 ax+by+c=0を表します。 点の座標はユークリッド座標(2つの数のリスト [x,y]) か、 または同次座標 (3つの数のリスト [x,y,z] で点 [x/z,y/z])を表す)です。戻り値は常に同次座標です。以下の説明の中では、特に断りなく、点の形式の引数は <point>で、直線の形式の引数は <line> で表します。<point> と <line> は両方とも3つの数のリストで表現することができるので、両者を区別する方法が必要になります。内部的には、リストは、それが幾何学的にどのような意味を持つのかというフラグを持っています。その情報は、 geotype(<list>) 演算子で得ることができます。この演算子は、 "Point", "Line", "None" のいずれかを返します。ベクトルが持つ幾何学的な意味に応じて、 draw 演算子は対応する図形を描きます。基本的な幾何学演算子2直線の交点:
|
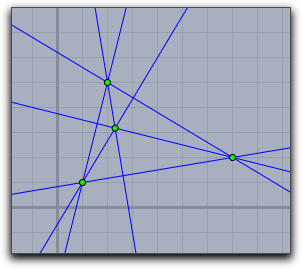 |
垂直なベクトル: perpendicular(<リスト>)
説明: もし
perp 演算子の引数が、2つの数からなるリスト1つだけとします。その場合は、リスト [a,b] は [-b,a] に変換されます。それは、もとのベクトルを 90° 回転したものです。三角形の面積: area(<点1>,<点2>,<点3>)
説明: この演算子は、<60point1>, <60point2>, <60point3> を3つの頂点とする三角形の面積を計算します。点の方向が反時計回りならば面積は正、時計回りならば面積は負になります。3点が同一直線上にあるときは面積はゼロです。
有用な線形代数演算子
線形代数で使う次の演算子は幾何でも有用です。特に3次元のベクトルに適用できます。 その状況 (行列の計算、内積など) については、ベクトルと行列 の節を参照してください。
3点の位置ベクトルの行列式: det(<ベクトル1>,<ベクトル2>,<ベクトル3>)
説明: この演算子は、3つの3次元ベクトル
<ベクトル1>, <ベクトル2>, <ベクトル3> からなる 3 × 3 行列の行列式を計算します。ベクトルと行列 の節にある一般的な行列式と異なり、この方法はパフォーマンスが優れています。2点の位置ベクトルの外積: cross(<ベクトル1>,<ベクトル2>)
説明: この演算子は、2つの3次元ベクトルの外積を計算します。外積は3次元ベクトルで、もとの2つのベクトルと垂直です。
変換とオブジェクトの型
オブジェクトの型: geotype(<リスト>)
説明: この演算子は、オブジェクトが明確な幾何学的意味を持つかどうかを決定します。戻り値は、文字列で
"Point", "Line", "None" のいずれかです。この演算子を、2つの数からなるリストに適用した場合は、常に
"Point"を返します。3つの数からなるリストに適用した場合は、このリストの内部フラグによって "Point", "Line", or "None" のいずれかを返します。シンデレラで描画した幾何オブジェクトであれば、常にそのフラグを有しています。 meet 演算子の戻り値は常に "Point" です。 join, parallel, perpendicular 演算子の戻り値は常に "Line"です。さらに、幾何学的意味は line と point 演算子によって明確に設定することができます。点の指定: point(<ベクトル>)
説明: この演算子は、3つの数のベクトルを、はっきりと
"Point"として位置づけます。引数が3つの数からなるベクトルでなければ無効です。直線の指定: line(<ベクトル>)
説明: この演算子は、3つの数のベクトルを、はっきりと
"Line" として位置づけます。引数が3つの数からなるベクトルでなければ無効です。点を複素数に変換: complex(<点>)
説明: この演算子は点の座標を複素数に変換します。ここで、ユークリッド座標系はガウスの複素数平面と同一視されます。点
[a,b] は複素数 a+i*bに変換されます。複素数を点に変換: gauss(<点>)
説明: この演算子は先ほどと逆です。複素数
a+i*b を2つの数のリスト [a,b] に変換します4点または直線の複比: crossratio(<ベクトル>,<ベクトル>,<ベクトル>,<ベクトル>)
説明: 4点の幾何複比を計算します。4点が共線であれば、通常の実数射影平面における複比が計算されます。4点が共線でなければ、複素射影直線の対応した点における複比が計算されます。共線的無限遠点に対しては2つの結果は同等です。
4つの数の複比: crossratio(<数>,< 数 >,< 数 >,< 数>)
説明: 4つの実数または複素数の複比 (A/B)/(C/D) を計算します。 とても有用な幾何学的不変量です。
幾何学変換と基底
代数的な方法で幾何の変換を扱うことができます。変換は 3 × 3 行列で表されます。実際の変換は、点の同次座標に変換行列を掛けて行われます。この変換行列を計算するためにいくつかの演算子があります。
線対称: linereflect(<直線>)
説明: <直線>に関して対称な点をを求める行列を返します。
例: 次のコードは直線 a を与えて、対称変換行列を作り、点C の同次座標に掛けて対称点を求めます。結果は緑色の点です。
m=linereflect(a); draw(m*C.homog);
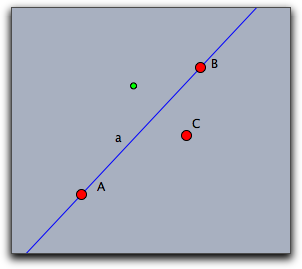 |
点対称: pointreflect(<点>)
説明:
<点> に関する対称点を求める行列を返します。平行移動: map(<点1>,<点2>)
説明: <点1> を <点2> に写す平行移動を表す行列を返します。
相似変換: map(<点1>,<点2>,<点3>,<点4>)
説明: <点1>を<点2>に、<点3>を<点4> に写す相似変換を表す行列を返します。
アフィン変換: map(<点1>,<点2>,<点3>,<点4>,<点5>,<点6>)
説明: <点1>を<点2>に、<点3>を<点4>に、<点5>を<点6> に写すアフィン変換を表す行列を返します。
射影変換: map(<点1>,<点2>,<点3>,<点4>,<点5>,<点6>,<点7>,<点8>)
説明: <点1>を<点2>に、<点3>を<点4>に、<点5>を<点6>に、<点7>を<点8> に写す射影変換を表す行列を返します。
Contributors to this page: Akira Iritani
.
Page last modified on Wednesday 07 of March, 2012 [10:47:08 UTC] by Akira Iritani.
The content on this page is licensed under the terms of the License.
Login