CalculusJ

計算

CindyScript は純粋に数的言語です。記号的計算は行いません。にもかかわらず、通常記号的システムだけが行えるようないくつかの手続きを行うことができます。たとえば、関数の微分や接線を計算することができます。この節では、これら２つの機能の使い方を例示します。

微分と接線

微分: d(<function>,<var>)

説明: この演算子は、第１引数 に与えられた関数の導関数を作ります。微分は標準的な実行変数 # についておこなわれますが、変数名を第２引数に指定します。次のコードが使用例です。



実行結果は次の図です。青の線がもとの関数 f(x) 、赤の線が第１次導関数 g(x) 、そして黒の線が第２次導関数 h(x)のグラフです。



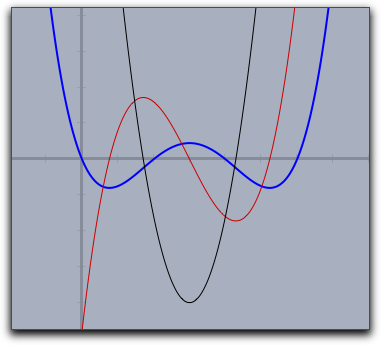第２次導関数は第１次導関数を微分したものです。しかし注意事項があります。微分演算子は完全に数の原則に基づいています。 f(x) が微分可能ならば、導関数は d(f(#),x) で定義されます。ここで、x が微分する変数を示しています。導関数の値は、式

(f(x+eps)-f(x-eps))/2eps

によって計算されます。 eps は十分小さい数です。これは、この点における実際の微分係数に十分近い値になります。しかし、連続して何度かこの演算子を使うと、かなり誤差を生じます。5回も微分すると結果は使えません。したがって第５次導関数ではもはや理にかなった計算はできません。


修飾子: 初期値として、上記の式の eps は 0.0001 に設定されています。この値は、高次導関数の信頼性と精度のバランス上十分理にかなった値です。この値は修飾子 eps-><number> によって変更することができます。

---

接線: tangent(<function>,<var>)

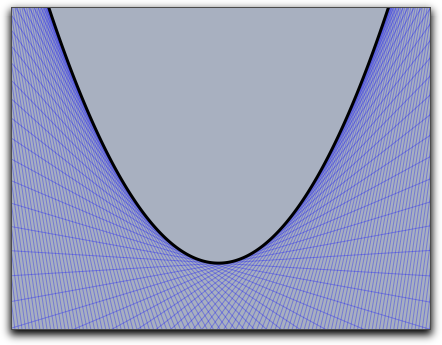
説明: この演算子は、微分とよく似ています。しかし、微分係数を計算する代わりに、ある点における接線の同次座標を計算します。 その点は第２引数で与えます。 次のコードでは、放物線のいろいろな接線を計算しています。




次の図が実行結果を示します。



tangent 演算子の戻り値は3次元ベクトルの同次座標です。加えて、直線の内部フラグが立っています。(幾何学演算子参照) そのため、自動的に直線が引かれるのです。

---

実数値を推測する: guess(<number>)

説明: 推測演算子は、CindyScript のなかでも、おそらく最も洗練されて強力な演算子の一つです。それは浮動小数点数から記号的意味を取り戻すのに使われます。 guess 演算子は入力として数を予想し、文字列を返します。文字列は入力された数を記述する記号的な式です。 guess 演算子は、次の形式の文字列を生み出そうとします。

a+b*sqrt(c),

ここで a, b, c は、約1000以下の分母と分子で表される有理数です。入力された数が十分な精度で表現できるならば、上記の形で表します。 そうでなければ、 guess 演算子はそのまま入力値を返します。

したがって、guess 演算子は２次方程式の解を発見するのに使うことができます。この演算子は、図形に隠された特性を見つけるのに時々役に立ちます。これを２,３の例で示しましょう。最初の図では、直線の傾きと2つの円の交点の座標が"推測されて"います。



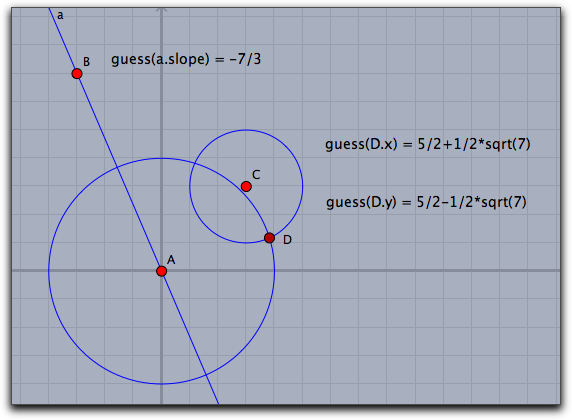入力された座標と半径が整数ならば、結果は平方根か比較的係数の小さな２次方程式の解です。次の２つの例は、推測の重要な使用例です。左は星形正五角形で２つの長さを比較しています。長さの比は正確に黄金比です。第２の例は単純な図形で２つの正方形の面積比の関係の面白さを表しています。



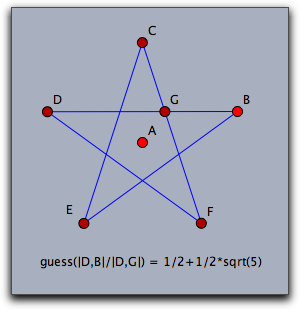
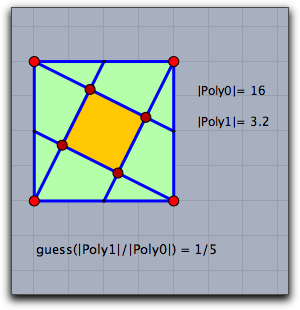
注意: guess 演算子の背後で働いているのは、いわゆる PSLQ と呼ばれるアルゴリズムです。実数 x,y,z が与えられたときに、整数関係 a·x+b·y+c·z=0　を発見する実に巧妙なアルゴリズムです。実数xが２次関係式の解であるかどうかを調べたいならば、 a+b·x+c·x²=0 の整数関係を探さなくてはなりません。これが、 guess 演算子が実装しているものです。解はその整数係数を使って再構成されます。

---

n次方程式の解: roots(<list>)

説明: roots 関数は、１変数の多項式からなる方程式の解を示します。低次の項から高次の項に向かって順に係数を与えます。結果は複素数のこともあります。


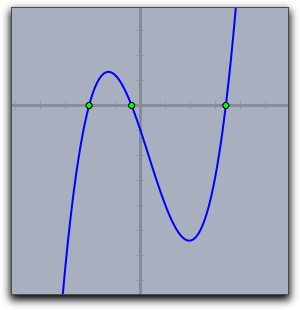
例: たとえば、方程式 1+x²=0 の解を求めたい場合は、単に roots([1,0,1]) とします。結果は複素数 [-0-i*1,-0+i*1] です。

　次のコードは、３次方程式の解を計算してグラフとともに表示します。