ShapesJシェイプ直線や多角形、円などの基本的な描画に加えて CindyScript によってこれらを結合した図形ーシェイプーを描くことができます。シェイプは直接は目に見えませんが、充填材やアウトラインの描画、クリッピングとして使えるでしょう。シェイプは和集合、積集合、補集合といった集合の論理演算によって作られます。ここでは、まず基本的な演算について説明し、そのあと、より精巧な例を示してこの機能について説明します。 シェイプの初歩円形のシェイプ:
|
|||||||||||||||||||||||||||||||||
<shape1>++<shape2> | 2つのシェイプの併合 | |
<shape1>~~<shape2> | 2つのシェイプの共通部分 | |
<shape1>--<shape2> | 2つのシェイプの差 | |
シェイプの使い方
シェイプは次に述べる3つの方法で使われます。充填と境界線描画、クリッピングです。
シェイプによる充填: fill(<shape>)
説明: この関数ではシェイプを与えられた色で塗りつぶします。
修飾子: つぎの修飾子が使えます。
| 修飾子: | 値の型 | 効果: |
color | [<実数1>,<実数2>,<実数l3>] | 塗りつぶす色をRGBで指定 |
alpha | <実数l> | 値 |
シェイプを描く: draw(<shape>)
説明: この関数はシェイプの輪郭線を描きます。
修飾子: この関数はよく使われるdraw()関数の拡張で、drawと同じ修飾子が使えます。
クリップパスの設定: clip(<shape>)
説明: この関数は、シェイプのクリップパスを設定します。これ以降に描画するものはすべてこのクリップバスで止められます。クリップパスは表現スタックに加えられますが、それは
grestore() あるいは greset() で取り除くことができます。例: 次の図はシェイプの使い方を示します。まず「点を加える」モードで点A〜Fをとっておきます。次のコードで3つの異なるシェイプが定義されます。1つの正方形と2つの円です。そして、それらが論理演算によって結合されています。充填とアウトラインです。小さなシェイプは、細い線でアウトラインが描かれています。
shape1=circle(E,4); shape2=circle(F,4); shape3=polygon([A,B,C,D]); color((0,0,0)); shape=shape1++shape2++shape3; fill(shape,color->(1,0.8,0)); draw(shape,size->3); draw(shape1); draw(shape2); draw(shape3);
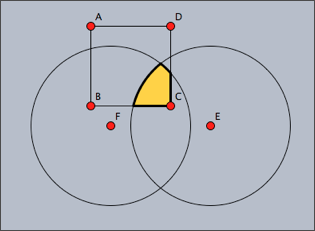
次の最初の図がこの結果です。ほかの3つの図は、それぞれ図の下に示した演算で作成したシェイプです。
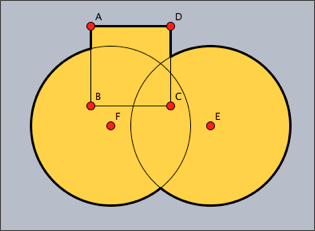 |  |
| shape1++shape2++shape3 | shape1~~shape2~~shape3 |
 | 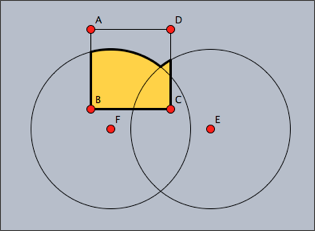 |
| shape1++shape2--shape3 | shape1++shape2~~shape3 |
次のコードはクリップパスの使い方を示します。「点を加える」モードで5つの点A,B,C,D,Eをとっておきます。スクリプトでは、まず4つの円を合併したシェイプを定義します。すると、このシェイプが、点Eを中心とした同心円のクリッピングパスとして働きます。
r=3; shape=circle(A,r)++circle(B,r)++circle(C,r)++circle(D,r); clip(shape); repeat(60,i, drawcircle(E,i/2,color->(0,.6,0),size->3); ); greset(); draw(shape,color->(1,1,1),size->2);
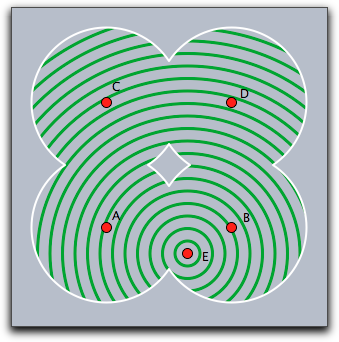 |
シェイプは、次の例に示すような反復系のオブジェクトにもなります。ただし、あまり複雑にすると破綻をきたしますので注意しておきます。複雑な形はシンデレラの動作を遅くしてしまいます。
a=complex(A); b=complex(B); z=complex(C); shape=circle((0,0),0); repeat(50, shape=shape++circle(gauss(a),|a-b|); a=a*z; b=b*z; ); fill(shape,color->(1,0.7,0)); draw(shape,color->(0,0,0),size->2);
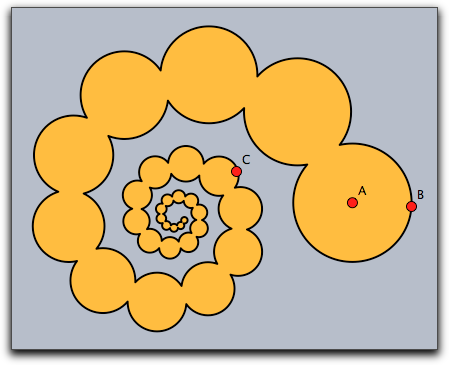 |
Contributors to this page: Akira Iritani
.
Page last modified on Tuesday 06 of March, 2012 [13:19:51 UTC] by Akira Iritani.
The content on this page is licensed under the terms of the License.
Login