Mirror
The mirror is a multipurpose tool for creating reflections at points, lines, or circles. The first mouse click selects the "mirror." The following clicks select the elements that should be reflected. Reflected elements are either points, lines, or conics. You can deselect the mirror by clicking on it a second time. Depending on the choice of the mirror, different actions are performed:
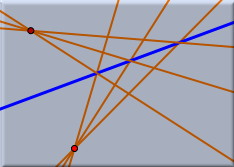
- If the mirror is a line then the usual reflection is taken. The mirror image of a point with respect to a line is a point that has the same distance to the line as the original point and lies on the perpendicular of the line that goes through the original point.
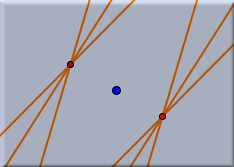
- If the mirror is a point then the reflection "at this point" is taken. The mirror image of a point with respect to a point is a point that has the same distance to the mirror-point as the original point and lies on the join of the mirror-point and the original point.
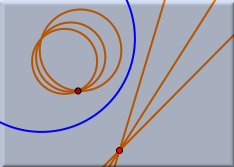
- If the mirror is a Euclidean circle, then the inversion at that circle is taken. The inverse of a point with respect to a circle is a point that lies on the join of the original point and the center of the circle. The distance of the inverse point to the center of the circle is such that the product of this distance and the distance from the center to the original point is the circle's radius squared.
Reflections of lines or conics are considered as pointwise reflections.
 | |
 | |
 |
| Reflection at a line | |
Reflection at a point | |
Inversion at a circle |
Synopsis
First select a mirror. Then select elements that should be reflected.
Caution
The definition a mirror image heavily depends the choice of the underlying geometry.