Interaction with GeometryJ

 print

幾何との連携


　CindyScript は Cinderella で作図した要素を操作することができます。要素の表示についての情報を得たり、それらを操作することができます。CindyScript で要素を削除したり、新たに作ったりすることもできます。

要素を動かす


CindyScript での計算は、シンデレラの図形の自由要素の位置をコントロールするのに使えます。その一つは、自由要素の位置をはっきりと指定することです。たとえば、Aが自由要素のとき、 A.xy=[1,1] は、その点を座標 [1,1] に設定します。 もう一つの方法は moveto 演算子を使って点を動かすことです。


自由要素を動かす: moveto(<geo>,<pos>)



説明: この演算子では <geo> に幾何の自由要素を、<pos> にこれを動かしたい位置を記述します。この演算子によって自由要素の動きをシミュレートします。

<geo> が自由点であれば、 <pos> は2つの数のリスト [x,y] か３つの数のリスト [x,y,z] です。 前者はユークリッド座標と解釈されます。後者は同次座標と解釈され [x/z,y/z] に点を打ちます。

<geo> が自由直線であれば <pos> は３つの数のリスト [a,b,c] でなければならず、直線 a*x + b*y + c = 0 に設定されます。

例: 次のコードは、幾何の要素をどのように動かせるかをまとめたものです。要素のデータに直接アクセスして動かすものも含みます。

//A は自由点
moveto(A,[1,4]);        // 点Aをユークリッド座標(1,4)に置く
A.xy=[1,4];             // 点Aをユークリッド座標(1,4)に置く
A.x=5;                  // A のx座標を 5 にする。y座標は変化しない
A.y=3;                  // A のy座標を 3 にする。x座標は変化しない
moveto(A,[2,3,2]);      // A を同次座標 [2,3,2] に置く
A.homog=[2,3,2];        // A を同次座標 [2,3,2] に置く

//a は自由曲線
moveto(a,[2,3,4]);      // a を同次座標 [2,3,4]に置く
a.homog=[2,3,4];       // a を同次座標 [2,3,4]に置く

//b は傾きつき直線
a.slope=1;              // 傾きを 1 にする

//C は半径が自由な円
C.radius=1;             // 半径を 1 にする



幾何要素のハンドル



動いた要素: mover()



説明: この演算子は、マウスによって今動かされた要素が何であるか(そのハンドル)を返します。




マウスのあるところの要素: elementsatmouse()



説明: この関数は、現在マウスカーソルの近くにある要素のリストを返します。

例: 次のスクリプトはちょっとした意味があります。このスクリプトをMouse Move スロットに置いて実行すると、マウスカーソルの近くにある要素が消えます。マウスカーソルが遠ざかればまた現れます。

apply(allelements(),#.alpha=1);
apply(elementsatmouse(),#.alpha=0);
repaint();




オブジェクトへのインシデント: incidences(<geo>)



説明: この関数は、幾何要素 <geo> とインシデントなすべての要素のリストを返します。



その名前の要素を取り出す: element(<string>)




説明: この関数は、 <string> の名前の幾何要素を返します。

例: element 演算子は、要素名が無効であるか、あるいはすでに使われているような場合に使われます。たとえば、i という名前の直線の色にアクセスしようとすると、i は虚数単位の名前として予約されているので、 i.color=1,1,1external link と書くことはできません。このような場合、次のように書きます。

element("i").color=[1,1,1]





幾何要素の生成と消去



自由点を作る: createpoint(<string>,<pos>)



説明: この演算子は <string> をラベルとする点を打ちます。点の位置は <pos> です。すでに同じ名前の点がある場合には新しく作らず、単に指定した位置に移動します。



幾何要素を作る: create(<list1>,<string>,>list2>)



説明: この演算子は、任意の幾何要素を作り出します。アルゴリズムがいくつか微妙な点を引き起こしますので、特別な用途に限られます。

第１引数の <list1>は生成する要素の名前のリストです。第２引数の <string> は幾何学的なアルゴリズムの内部的な名前です。第３引数の <list2> は、定義のために必要なパラメータのリストです。
次の表で、いくつかの例を示します。

create(["A"],"FreePoint",[[1,1,1]]);
create(["B"],"FreePoint",[[4,3,1]]);
create(["a"],"Join",[A,B]);
create(["X"],"CircleMP",[A,B]);
create(["Y"],"CircleMP",[B,A]);
create(["P","Q"],"IntersectionCircleCircle",[X,Y]);
create(["b"],"Join",[P,Q]);
create(["M"],"Meet",[a,b]);


この一連のコードで、次の図のように幾何要素を作ります。６番目の命令で円の交点を作るとき、２つの点の名前のリストがなければなりません。



幾何要素を作るときの正しいパラメータについては、次に述べる algorithm と inputs 関数によって得られます。



幾何要素の消去: removeelement(<geo>)



説明: 幾何要素を、それに関連するものも含めて消去します。


幾何要素を構成する要素: inputs(<geo>)



説明: この関数は、幾何要素 <geo> を定義するために必要な要素のリストを返します。それらは幾何要素のほか、数やベクトルであるかも知れません。



幾何要素の作図手順: algorithm(<geo>)



説明: この関数は <geo> の作図手順を文字列で返します。

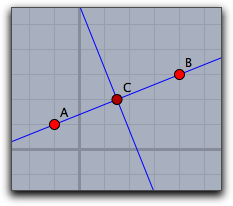
例: 次のスクリプトはすべての要素に対してその作図手順を示します。

els=allelements();
data=apply(els,([[#.name],algorithm(#),inputs(#)]));


　垂直二等分線の作図手順が次のように出力されます。:

 [[["A"],"FreePoint",[[4,4,-4]]],
  [["B"],"FreePoint",[[4,-3,1]]],   
  [["a"],"Join",[A,B]],
  [["C"],"Mid",[A,B]],
  [["b"],"Orthogonal",[a,C]]
]





要素の属性へのアクセス


　色や大きさといった、要素の属性は .color, .size などのオペレータでアクセスできます。しかし、要素にはたくさんの属性があります。それらにアクセスするには次の関数を用います。


すべての属性のリスト: inspect(<geo>)



説明: 幾何要素の属性のリストを返します。

例: inspect(A) とすると、自由点 A の属性名が次のようにリストアップされます。

[name,definition,color,color.red,color.blue,color.green,alpha,visibility,
drawtrace,tracelength,traceskip,tracedim,render,isvisible,
text.fontfamily,plane,pinning,incidences,labeled,textsize,textbold,textitalics,
ptsize,pointborder,printname,point.image,
point.image.media,point.image.rotation,freept.pos]




変更可能な属性へのアクセス: inspect(<geo>,<string>)



説明: 変更可能な任意の属性にアクセスします。

例: 点 A の色に、 inspect(A,"color") によってアクセスします。



変更可能な属性を設定する: inspect(<geo>,<string>,<data>)



説明: 変更可能な属性の値を設定します。

例: 点 A の色を inspect(A,"color",(1,1,1)) によって白に設定します。



再描画をする: repaint()



説明: この関数は描画している図を強制的に再描画します。これは、スクリプトが図の更新を必要とするときに実行されます。この関数は draw あるいは move スロットにおいてはいけません。


再描画その２: repaint(<real>)


説明:repaint命令を、パラメータで与えられたミリ秒だけ遅らせて実行します。



軌跡上の点: locusdata(<locus>)



説明: この関数は、<locus>によって与えられる軌跡上の点の xy-座標のリストを返します。

Contributors to this page: Akira Iritani .
Page last modified on Friday 26 of August, 2016 [11:29:35 UTC] by Akira Iritani.

The content on this page is licensed under the terms of the License.

similar
Menu
 Home
[-] Wiki [+]