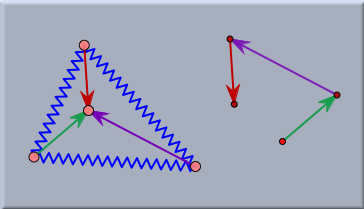
Geometry and CindyLabJ幾何学とCindyLabある意味では、このセクションはシンデレラのユーザーにとってはその機能を思い出してもらう程度のものかもしれません。 CindyLab では、すべての質点は幾何学的な点であり、バネや反射壁や床は直線や線分であるということです。したがって、幾何学的な構造によって CindyLab の実験装置を強化することがいつでも可能です。これらの幾何学的な構造は実験の正確な意味を分析するのに有益なことがあります。このことを3つの小さな例で示します。 例 1: 力のつりあい力がつりあっているとき、質点は加速しません。しかし、そのような場合、どの質点にも力がかからないことを意味します。これはまた、いくつかの粒子に及ぼす力の和がゼロであるともいえます。次の実験では、ゴムバンドとバネでできている簡単な網が、これを例証しています。青い三角形のバネがあります。各頂点は、中央の粒子とゴムバンドでつながっています。最初は、ゴムバンドの長さと方向は任意かもしれません。 しかしながら、シミュレーションの始めにすこし摩擦力を加えてやることによって、つりあいの状態になるようにするならば、内部の頂点でゴムバンドによる力は相殺されなければなりません。もし、すべてのゴムバンドが同じバネ定数を持っているならば、ゴムバンドを表す3つの線分は、平行移動によって(力の合計がゼロになる)三角形を作ることができます。
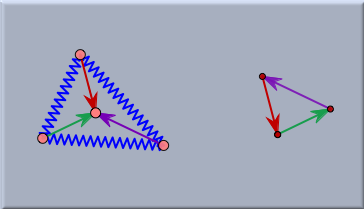
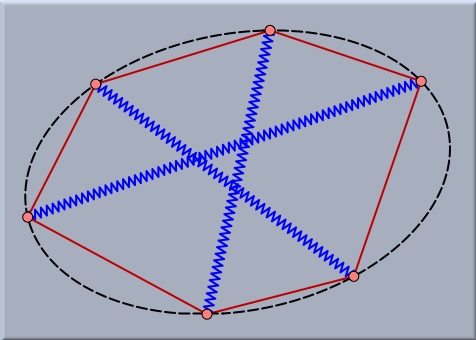
これは、3つの線分を平行移動によって補助的な図を作ることで簡単にテストできます。(図の右方) 開始時点ではこの3つの矢線は必ずしもつながっている必要はないことがわかるでしょう。2番目の図は、3つの端が自動的に完全な三角形をつくるつりあい状態にあることを示します。 ときどき、大変びっくりするような興味深い関係がつりあった状態の上に起こります。たとえば、次の図は6本のゴムバンドで囲まれる3本のバネの状況を表します。ゴムバンドには任意のバネ定数があるかもしれません。つりあっているとき、6つの頂点は自動的に楕円上にきます。
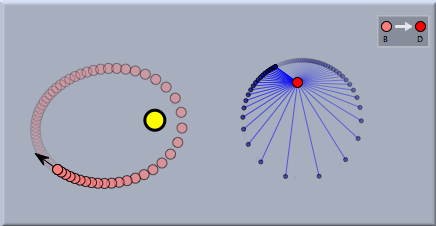
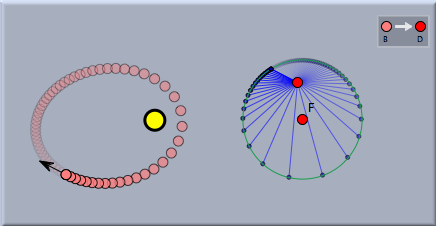
例 2: 惑星の動き二体システムの惑星運動に、あまり知られていませんが驚くべき幾何学的特性があります。すでに述べたように、恒星の周りを回っている惑星は楕円軌道を描きます。惑星の速度を考えると、恒星の近くでは速く、遠くでは遅くなります。また、動いている間、速度の方向が変わります。シンデレラでは速度ベクトルの様子をはっきりと調べることが簡単にできます。まず 恒星 と、 速度を持つ質点を加えます。シミュレーションを始めると、惑星はケプラー楕円に沿って動きます。 それから、自由点を加え、惑星からこの点へ変換 を定義します。これで、速度ベクトルをこの点に写し、速度ベクトルの動きとは独立した図を描くことができます。
速度ベクトルの軌跡を見ると、円だと推測されるでしょう。この推測を少なくとも視覚的に実証するのは簡単で、自由な円を加え、アニメーションが動いている間速度ベクトルの軌跡にマッチするようにしてやればいいのです。次の図は、それがどのくらいうまくマッチしているかを示します。
例 3: 金門橋にかかる力次の図は、重力の節で示されている例です。ここでは金門橋の写真が背景に読み込まれています。CindyLab を使って、橋のケーブルにかかる力の分布をシミュレーションします。シンデレラは写真の遠近感を出すのに使われます。物理シミュレーションの結果を写真の上に写すには 射影変換 を使います。重力を適正な値に調整することによって、この状況が橋をささえるケーブルの形状に似ていることが示されます。
Contributors to this page: Akira Iritani
. The content on this page is licensed under the terms of the License. |
Login |