Elementary MechanicsJ

力学のシミュレーション

基本的なしくみ

加速度 は 力 を 質量で割ったものに等しい

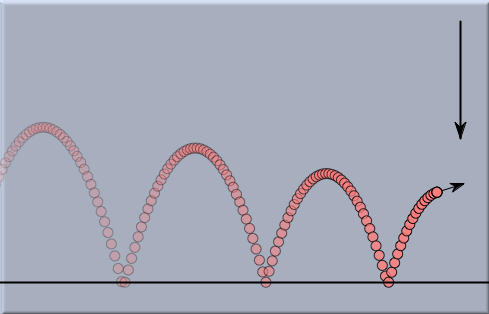
　この単純な法則は、力の影響を受けている質点(粒子)の動きを理解するための鍵です。 質点というのは、電子や球体ばかりでなく惑星も含みます。 力にはいろいろな種類があります。 電磁気力、引っ張られたバネ、惑星間の重力などです。 質点のタイプや力のタイプとは無関係に、上記の法則はどのように速度が変化するかを示します。

加速度は単位時間における速度の変化です。上記の法則により、単純な、しかし重要な結果を得ます。 もし力が加えられなければ、粒子はその速度を保持し、同じ方向に永遠に同じ速さで移動します。 力が加えられると、粒子は方向を変えたり、速くなったり、遅くなったりします。それらは、引き寄せられたり反発したりするように見えます。

重力が働くときのボールの動き

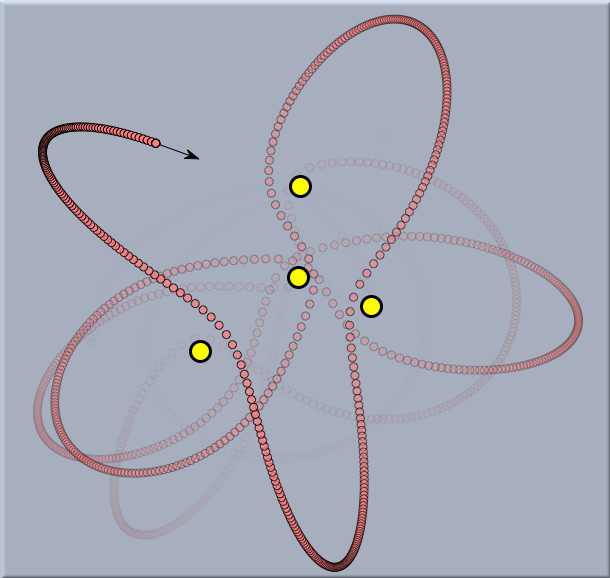
　原則として、すべての力の働く粒子の初期位置と初速度がわかっていれば、粒子の運動の結果を正確に知ることができます。もしも正しい数学的形式を適用するならば、そのようなシステムは微分方程式につながります。微分方程式は、システムの動きを数学的に記述するものです。ただ、残念なことに、小さな物理システムであっても微分方程式だけでははっきりと解決できません。次のシステム(4つの恒星の影響を受ける惑星)で見られるように混沌とした振る舞いを見せるかも知れません。

いくつかの恒星の影響下にある惑星の動き

　それでも、数値的な方法で、そのような微分方程式に取り組むことができます。弧の数値的方法では、別々の方法で連続システムをモデル化します。つまり、時間内の別々の点で位置、速度、力を調べます。 ある時刻tにおける状況から、間隔Δt(デルタt)後の位置と時間を推定します。時刻(t+Δt)における推定値を用いて、次の時刻における推定値を計算します。この方法により、位置と速度の異なる道筋が生成されます。もちろん、そのような道筋は正確な物理的現実にはマッチしません。しかしながら、推定値が良好で、時間間隔Δが大きくなければ、物理的に理にかなった近似値が得られます。さらに、良好な数値的解は、たいていの場合、時間間隔をゼロに近づければ、計算結果が物理的現実により近くなるという特性を持っています。.

---

続ける --> シンデレラと物理学