Add a ParallelAdd a Parallel
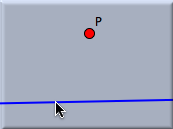
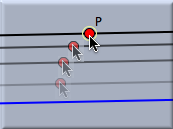
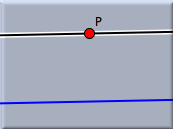
The figures below show the three stages during the construction of a parallel. Here the new point will be bound to the existing point P.
SynopsisAdd a parallel mode creates a parallel with a press–drag–release sequence. CautionThe behavior of this mode is dependent on the geometry that is chosen. While in Euclidean geometry there is always exactly one parallel, in non-Euclidean geometries the number of parallels is subject to the definition of parallelity. Depending on the underlying "philosophy," in hyperbolic geometry there can be infinitely many parallels, from an incidence-geometric viewpoint, or there can be exactly two parallels, from an algebraic or measurement-based point of view. Cinderella takes the algebraic point of view: A parallel to a line L is a line that creates a zero angle with L. So in hyperbolic geometry the mode produces exactly two parallels.
In elliptic geometry the usual viewpoint is that there are no parallels at all. However, from an algebraic standpoint there exist such parallels. It is just that they have complex coordinates. In other words, they will never be visible. Cinderella constructs these parallels, and they are invisible but are nevertheless present in the Construction Text view. From there they can be accessed for further constructions.
Contributors to this page: Richter
,
Kohler
,
Kortenkamp
and
Kramer
. The content on this page is licensed under the terms of the License. |
Login |